
| chercheursduvrai.fr |
 Aide Aide
 Recherche Recherche
 Membres Membres
 Calendrier Calendrier
|
| Bienvenue invité ( Connexion (Log In) | Inscription (Register) ) | Recevoir à nouveau l'email de validation |

 To view this board in english, you must be registered.
To view this board in english, you must be registered.| Pages: (3) [1] 2 3 ( Aller vers premier message non lu ) |    |
|
Ecrit le: Lundi 15 Juin 2015 à 14h00

|
|||||
 Expert(e)       Groupe: Membres Messages: 2108 Membre n°: 10443 Inscrit le: 08/11/2013 |
Dans son film GIZEH 2005 DE PATRICE POOYARD, JACQUES GRIMAULT, annonce l'introduction d'un autre nombre irrationnel en plus de pi et phi, mais sans le nommer, grâce à un livre que j'ai acheté un peu par hasard, à un bon libraire Théorie des formes et des champs de Cohérence de Jacques Ravatin, (je n'ai que le tome II) https://fr.wikipedia.org/wiki/Nombre_plastique (déjà posé par LeTigreFr )
où il mentionne ce qu'il nomme le nombre radiant mes recherches m'ont appris qu'il se nomme souvent nombre plastique, peut être en lien avec l'architecture, ou aussi nombre d'argent, mais c'est plus trompeur, car d'autres équations utilisent ce même nom. D'ailleurs il a été proposé un autre nom qui pourrait bien convenir le nombre de Platine. (pouquoi pas, c'est vrai que cela devient confus) et à priori, il n'y a pas une série mais au moins deux, qui ont été étudiées et y sont associées, les série de Padovan, qui correspond au livre de Ravatin, dont la série 1,1,1,1,2,2,3,4,5,7,9,12,16,21,28,37,49,65,86,114,151,200,265,351,465,616,1081,1432,1897,2313, etc et la série de Périn qui n'a peut qu'un intérêt purement mathématique. Je vous laisse découvrir le nombre radiant psi http://serge.mehl.free.fr/anx/suite_padovan.html http://villemin.gerard.free.fr/Wwwgvmm/Ite...ovan.htm#depart et est ce que cela peut être un homologue du nombre phi et puis il y a une ressemblance surprenante entre http://openclassrooms.com/forum/sujet/nomb...ationnels-56423
parmi les écritures de la solution: et |
||||
|
Ecrit le: Lundi 15 Juin 2015 à 15h08

|
|
 Administrateur       Groupe: Administrateurs Messages: 5756 Membre n°: 1 Inscrit le: 04/08/2002 |
Alors si les paris sont ouverts, je parlerai quand à moi du nombre d'Euler, e.
En effet il parle d'un nombre connu de nous depuis 200 ans. Le nombre d'Euler a un peu plus de 200 ans et il est transcendant, comme pi. Voir ici la découverte du nombre d'Euler, par exemple: http://www.maths-et-tiques.fr/index.php/hi...-celebres/euler http://www.maths-et-tiques.fr/index.php/hi...res/le-nombre-e -------------------- "L’homme sage n’est pas comme un vase ou un instrument qui n’a qu’un usage ; il est apte à tout."
"Appliquez-vous à garder en toute chose le juste milieu." Confucius |
|
Ecrit le: Lundi 15 Juin 2015 à 15h55

|
|
|
Expert(e)       Groupe: Membres Messages: 1247 Membre n°: 303 Inscrit le: 15/06/2007 |
Champs de cohérences et incohérences , Jacques Ravatin et Daniel Zakrzynski ( LE GENERATEUR D'ETOILES ) bouquin absolument fabuleux , basé sur quelques théories de Tesla dont une des plus puissante , nous expliquant que l’énergie est partout dans tous les coins de l'univers et que l'on peut la "pomper " absolument partout ....plus les théories de Morey et de Boutard , dont une des principales théorie extraordinaire sur la matérialisation de la parole surtout a partir de l'alphabet Hébraïque ....
Ce que devait pratiquer le christ , de la même façon que nous respirons , ce qui' n'est qu'un réflexe moteur pour nous , et la matérialisation par le verbe pour le Christ , un acte hautement spirituel étant dans sa nature propre ... Le générateur d’étoile , absolument fabuleux |
|
Ecrit le: Lundi 15 Juin 2015 à 16h10

|
|
 Expert(e)       Groupe: Membres Messages: 2108 Membre n°: 10443 Inscrit le: 08/11/2013 |
Pour les paris, ce ne serait donc pas gagné pour moi, car pour ma part d'après tout ce que j'ai pu trouver, les liens étaient trop récents. et bien plus récents en tout cas que deux siècles,
donc, en effet tu as sûrement le meilleur filon. je vais voir si cela m'inspire, pour ne pas oublier de réviser avant que Jacques n'ait réalisé la série de films! Je poursuis encore un peu mon lien précédent... Pour vérifier le côté improbable de la suite du nombre radiant, on peut vérifier que la construction en triangle fonctionne bien avec le multiplicateur, j'ai essayé avec 10 chiffres significatifs, 1,324717957 sur ma calculette en reprenant les cotés du triangle de côte 5*psi =6,623, encore éloigné de 7, mais si on continue jusqu'aux derniers termes de la suite de mon précédent post, ci dessus, la précision devient très bonne, par exemple, dans la fin de la liste 1432*psi=1896,996... qui est tout prêt de 1897 donc cela correspond et ressemble vraiment à l'esprit des séries de Fibonaci et de son fameux nombre d'or. Mathématiquement, cela fonctionne un peu de la même façon, et je ne serais pas étonné si cela est en lien aux énergies subtiles comme Jacques Ravatin tentait de le montrer dans ses livres... Petite pensée personnelle: Si l'univers est de toute façon régi par les mathématiques, c'est que ce n'est donc pas l'homme qui a inventé les mathématiques la Nature en fait tous les jours, un peu tout comme Mr Jourdain, fait de la Prose. |
|
Ecrit le: Lundi 15 Juin 2015 à 16h38

|
|
 Administrateur       Groupe: Administrateurs Messages: 5756 Membre n°: 1 Inscrit le: 04/08/2002 |
Voir le vieux débat d'Alain Connes et Jean-Pierre Changeux au sujet de savoir si l'univers est mathématique et c'est pourquoi l'homme en perçoit dans tous les phénomènes physiques, ou si c'est les cerveaux humains qui fonctionnent de façon sous-jacente dans le mathématisable et qui tel un filtre ne voient les choses que sous cet angle sans que rien d'intrinsèquement mathématique n'existe dans la nature (le cerveau invente alors une perception mathématique de choses chaotiques ou qui du moins n'ont pas forcément la mathématique en eux, il ré-ordonné pour donner du sens suivant sa façon interne de décoder les choses; comme une illusion globale de la réalité remise en forme mais par tous les cerveaux de la même façon car on est tous construits identiquement: je réactualiserai en parlant non pas du cerveau, mais du mental qui crée l'illusion d'un monde là où n'existe que des choses qui ne sont pas comme on le croit). C'est un vieux débat.
http://www.amazon.fr/Mati%C3%A8re-%C3%A0-p...x/dp/2738108156 http://www.franceculture.fr/oeuvre-matiere...e-changeux.html -------------------- "L’homme sage n’est pas comme un vase ou un instrument qui n’a qu’un usage ; il est apte à tout."
"Appliquez-vous à garder en toute chose le juste milieu." Confucius |
|
Ecrit le: Lundi 15 Juin 2015 à 19h02

|
|||
 Expert(e)       Groupe: Membres Messages: 3069 Membre n°: 10219 Inscrit le: 30/11/2012 |
-------------------- Supplions inlassablement Dieu d’accroître en nous deux vertus : l’amour et la crainte. Car l’amour nous fera courir sur les voies du Seigneur et la crainte nous incitera à regarder où nous posons le pied. L’un nous fera apprécier les réalités du monde pour ce qu’elles sont véritablement, l’autre nous mettra en garde contre toute négligence. Padre PIO |
||
|
Ecrit le: Mardi 16 Juin 2015 à 07h27

|
|
 Expert(e)       Groupe: Membres Messages: 3069 Membre n°: 10219 Inscrit le: 30/11/2012 |
Des nombres harmoniques tiens tiens ... la somme des inverses là encore
https://fr.wikipedia.org/wiki/Nombre_harmonique GÉOM. Division harmonique d'une ligne. ,,Division telle que les segments soient dans un rapport non fractionnaire`` (Littré). Proportion harmonique. ,,Proportion dans laquelle le premier terme est au troisième, comme la différence du premier et du second est à la différence du second et du troisième`` (Littré). Fonction harmonique. Toute fonction harmonique et régulière à l'intérieur d'une sphère est développable en série de Mac-Laurin (Painlevé, Résist. fluides non visqueux,1930, p. 63). Faisceau harmonique. Considérons un faisceau harmonique. Les points de rencontre A, B, C, D des rayons (...) de ce faisceau avec une sécante quelconque forment une division harmonique (ABCD) (Roux,Miellou, Géom.1946, p. 184). − En partic. ANTIQ. Nombres harmoniques. Des nombres harmoniques, dont le plus parfait étoit le quatre, selon Pythagore, et le cinq, d'après Saint-Pierre, formoient dans les choses une arithmétique mystérieuse, d'où découloient les secrets et les grâces de la nature (Chateaubr., Essai Révol., t. 1, 1797, p. 268). Rem. Harmonique se distingue de harmonieux par le fait que le premier exprime ce qui fonde l'harmonie, une relation, un rapport congruent, une correspondance cohérente (suff. -ique) et le deuxième le résultat de ce rapport, la satisfaction, l'agrément esthétique (suff. -eux). 5. 1732 terme d'acoustique, son harmonique (Trév.). Empr. au lat.harmonicus « bien proportionné, harmonieux », empr. du gr. α ̔ ρ μ ο ν ι κ ο ́ ς terme de mus. « conforme aux lois des accords » -------------------- Supplions inlassablement Dieu d’accroître en nous deux vertus : l’amour et la crainte. Car l’amour nous fera courir sur les voies du Seigneur et la crainte nous incitera à regarder où nous posons le pied. L’un nous fera apprécier les réalités du monde pour ce qu’elles sont véritablement, l’autre nous mettra en garde contre toute négligence. Padre PIO |
|
Ecrit le: Mardi 16 Juin 2015 à 07h55

|
|
|
Expert(e)       Groupe: Bannis Messages: 453 Membre n°: 10322 Inscrit le: 24/03/2013 |
Très intéressant, LeTigreFr,
Peux tu développé ? Merci |
|
Ecrit le: Jeudi 13 Août 2015 à 21h59

|
|
|
Expert(e)       Groupe: Membres Messages: 519 Membre n°: 10713 Inscrit le: 06/02/2015 |
Je viens de survoler ce post et de tilter sur ceci: radiant=rayon!!!!!!
C'est évident, tout ce qui traite des RADIAtions doit être lié au rayon, la moitié de PI! Cette idée est bonne, nos maths peuvent rapidement être difficile si toutes nos opération découlent de PI qui est indivisible, aussi on pose une deuxième UNIté en plus de PI, PHI, le radiant, qui est égal à PI/2, d'ailleurs sa graphie, avec le H, nous indique que c'est lui le véritable transcendant, celui qui lie le cercle et le carré PI au triangle PHI, et PHI est défini en fonction de PI, c'est la manière propre de faire des maths en effet! 3 Axes réunis en un seul, 1 axiome, 1 trinité Je ferais quelques dessins dans les jours qui viennent si le besoin se fait sentir -------------------- Le signe de ton ignorance, c’est la profondeur de ta croyance en l’injustice et en la tragédie. Porté à mon attention par zone-7.net, auteur original Richard Bach dans le livre "Illusions-Récit d'un messie récalcitrant" |
|
Ecrit le: Mercredi 26 Août 2015 à 17h12

|
|||
 Expert(e)       Groupe: Membres Messages: 2108 Membre n°: 10443 Inscrit le: 08/11/2013 |
Petit retour sur Euler, mais cette foi, pas au sujet d'un nombre irrationnel mais suite à ce lien, j'ai vu cette équation très particulière concernant le solides de Platon http://therese.eveilleau.pagesperso-orange...xtes/platon.htm
vérifié et tout à fait exact, mais on peut se demander par quelle logique, il a pu la concevoir? |
||
|
Ecrit le: Jeudi 27 Août 2015 à 08h07

|
|
|
Expert(e)       Groupe: Bannis Messages: 453 Membre n°: 10322 Inscrit le: 24/03/2013 |
@ p'titjoule
L'équation F+S=A+2 ne marche que pour des volumes tétraèdres Tu prends un plan fermé, il a 1F, 4S et 4A Tu prends une sphère, elle a 1F, 0S et 0A A moins de prendre les faces externes et les faces internes, et là oui ça marche pour ces cas. Mais si tu prends un cube, il a 6F, 8S et 12A, et là, ça ne marche qu'avec les faces externes C'est donc surement par étude de plusieurs figures qu'il a obtenu cette équation ; mais je ne suis pas spécialiste mathématique ! |
|
Ecrit le: Jeudi 27 Août 2015 à 09h18

|
|||
|
Expert(e)       Groupe: Membres Messages: 519 Membre n°: 10713 Inscrit le: 06/02/2015 |
Tout juste phil40, seulement si tu prêtes attention à ton vocabulaire, le verso d'un plan fermé est une face externe, non une face interne! Idemn pour la sphère (surface), qui n'est pas une boule (solide)! Le cube en revanche est bien un solide, ses faces internes sont bien des faces internes, il n'y a donc pas lieu de les compter! Donc un plan fermé à 2F, 4S et 4A Quand à la sphère, il faudrait faire une longue démonstration mais pour arriver à vérifier le théorème d'Euler, il faut considérer S et A comme quasi-infini. C'est la transformation qui revient à dire qu'un cercle est un polygone équilatéral avec une infinité de côtés, mais bien sûr une relation lie le nombre de A au nombre de S et au nombre de F, c'est le théorème d'Euler! Tu vois mieux p'titjoule la logique toute bête qui est à l'origine du théorème d'Euler? -------------------- Le signe de ton ignorance, c’est la profondeur de ta croyance en l’injustice et en la tragédie. Porté à mon attention par zone-7.net, auteur original Richard Bach dans le livre "Illusions-Récit d'un messie récalcitrant" |
||
|
Ecrit le: Jeudi 27 Août 2015 à 10h45

|
|||||||||||||||||
 Expert(e)       Groupe: Membres Messages: 2108 Membre n°: 10443 Inscrit le: 08/11/2013 |
Pour mieux se représenter, voila ce que ça donne pour chacun des solides on peut aussi écrire cette équation ainsi F+S-A=2
mais j'ai fait le calcul sur deux minéraux à facettes
et bien, à priori, la formule semble se confirmer pour bien des volumes à facettes, peut être même tous! |
||||||||||||||||
|
Ecrit le: Jeudi 27 Août 2015 à 10h57

|
|
 Expert(e)       Groupe: Membres Messages: 3939 Membre n°: 10047 Inscrit le: 07/11/2011 |
Marche pas pour les cylindres, si ?
-------------------- « No matter where you are, Look for the brightest star, Believe it is true, My soul is smiling at you", FastWalkers
|
|
Ecrit le: Jeudi 27 Août 2015 à 11h19

|
|
 Expert(e)       Groupe: Membres Messages: 2108 Membre n°: 10443 Inscrit le: 08/11/2013 |
si, ça marche très bien!
donc... euh: 3f-2a-2 = (-) 1 sommet |
|
Ecrit le: Jeudi 27 Août 2015 à 11h44

|
|
|
Expert(e)       Groupe: Bannis Messages: 453 Membre n°: 10322 Inscrit le: 24/03/2013 |
ça est intéressant !
mais pour sphère et cylindre, ..., il faut décomposer une surface cylindrique en une succession de surface plane, ce qui donne une infinité de faces, de sommets et d'arrêtes, et là, cela voudrait dire que la limite de l'équation F+S-A=2 tendrait vers 2 quand F, A et S tend vers l'infini Autrement dit, la forme +"infini"+"infini"-"infini" tend vers 2 ; or ceci est une forme indéterminée en math ! Qu'en disent les matheux ? |
|
Ecrit le: Jeudi 27 Août 2015 à 12h23

|
|
|
Expert(e)       Groupe: Membres Messages: 519 Membre n°: 10713 Inscrit le: 06/02/2015 |
Héhé vous vous prenez la tête les amis, je suis parti faire quelques dessins pendant que vous discutiez, les Grecs nous mettront tous d'accord!
Un cercle PEUT et DOIT être considéré comme un polygone EQUILATERAL avec une infinité de côté. C'est cette méthode qui permet de calculer une longueur courbe en fonction d'une longueur droite. Le plus simple des polygones équilatéraux/cercle est le triangle équilatéral, puis le carré, puis le pentagone,... Voici ce qu'est un cercle: 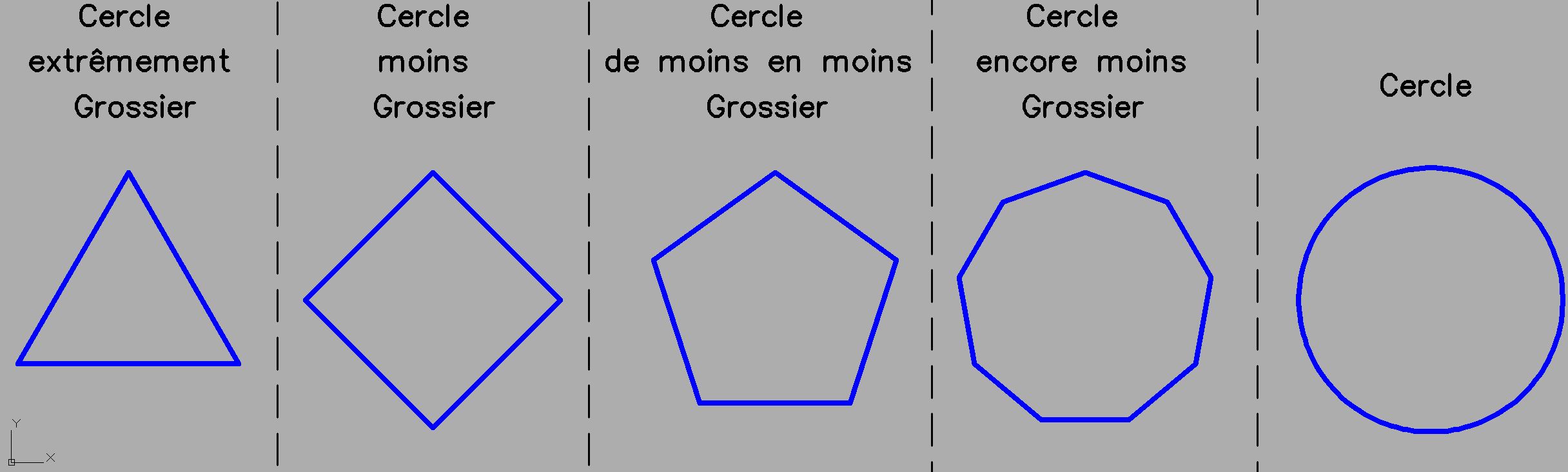 Maintenant, pour comprendre comment un cylindre peut vérifier la formule d'Euler, on passe ça en 3D: 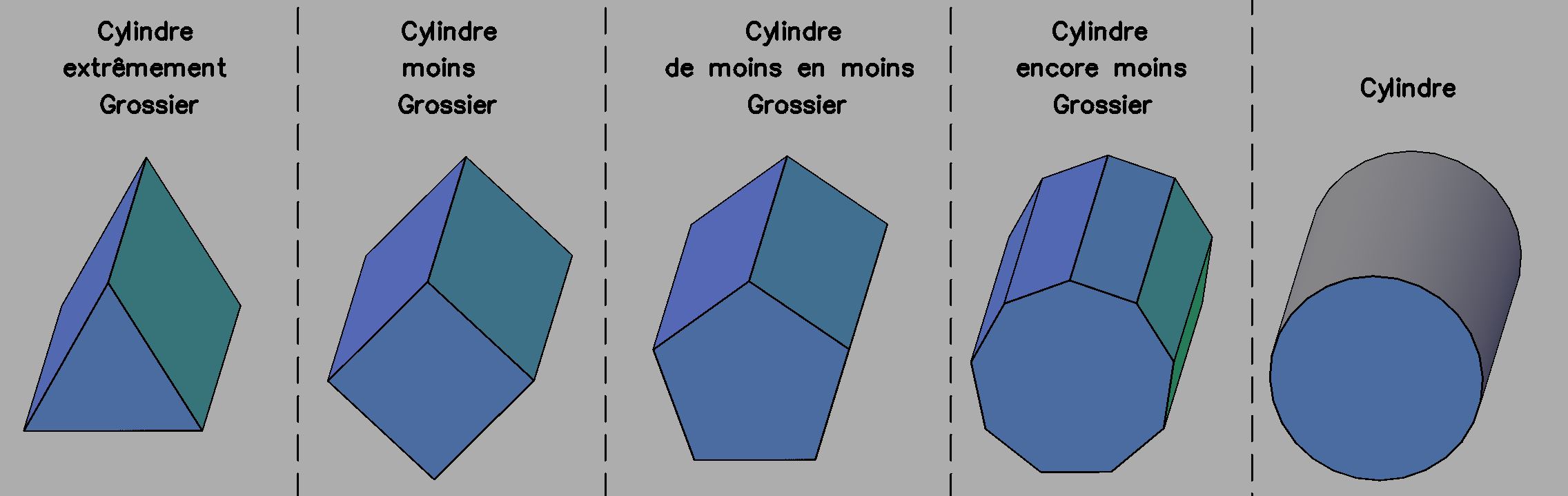 Formule d'Euler: Cylindre "triangulaire": 5F+6S-9A=2 Cylindre "rectangulaire": 6F+8S-12A=2 Cylindre "pentagonal": 7F+10S-15A=2 ... Vous pouvez continuer ainsi jusqu'à l'infini, le cylindre vérifie toujours la formule d'Euler! -------------------- Le signe de ton ignorance, c’est la profondeur de ta croyance en l’injustice et en la tragédie. Porté à mon attention par zone-7.net, auteur original Richard Bach dans le livre "Illusions-Récit d'un messie récalcitrant" |
|
Ecrit le: Jeudi 27 Août 2015 à 12h45

|
|
|
Expert(e)       Groupe: Membres Messages: 519 Membre n°: 10713 Inscrit le: 06/02/2015 |
Notez aussi la superbe suite qui se met en place: à chaque fois que l'on rajoute une arêtes sur la figure 2D (pour passer de triangle à carré, de carré à pentagone,...); sur la figure 3D cela se traduit par +1F, +2S, +3A
-------------------- Le signe de ton ignorance, c’est la profondeur de ta croyance en l’injustice et en la tragédie. Porté à mon attention par zone-7.net, auteur original Richard Bach dans le livre "Illusions-Récit d'un messie récalcitrant" |
|
Ecrit le: Jeudi 27 Août 2015 à 16h48

|
|
|
Expert(e)       Groupe: Bannis Messages: 453 Membre n°: 10322 Inscrit le: 24/03/2013 |
Ok jumab,
Tu es d'accord qu'un cylindre a une infinité de faces, sommets et arrêtes Peut-on noté qu'un cylindre a n*Faces, donc (n+1)*Sommets et (n+2)*Arrêtes, donc l'équation deviendrait : nF+(n+1)S-(n+2)A=2 : la suite ainsi noté n'est pas exacte ! Il faut trouver quelle est la relation entre F,S et A pour trouver quel est le bon réel multiplicateur Il faut l'écrire différemment |
|
Ecrit le: Jeudi 27 Août 2015 à 18h19

|
|
|
Expert(e)       Groupe: Membres Messages: 519 Membre n°: 10713 Inscrit le: 06/02/2015 |
Facile l'ami!
Relation d'Euler, travail sur les solides (la relation d'Euler fonctionne différemment dans le travail sur les aires): Le plus simple des solides est le tétraèdre. Relation d'Euler dans un tétraèdre: 4F + 4S - 6A =2 Soit un solide à n faces, avec n ≥ 4 (sinon ce n'est pas un solide!) Alors, S= 4 + (n - 4)*2 Et A = 6 + (n - 4)*3 Et un petit tableau de vérif pour prouver la validité de mes dires: 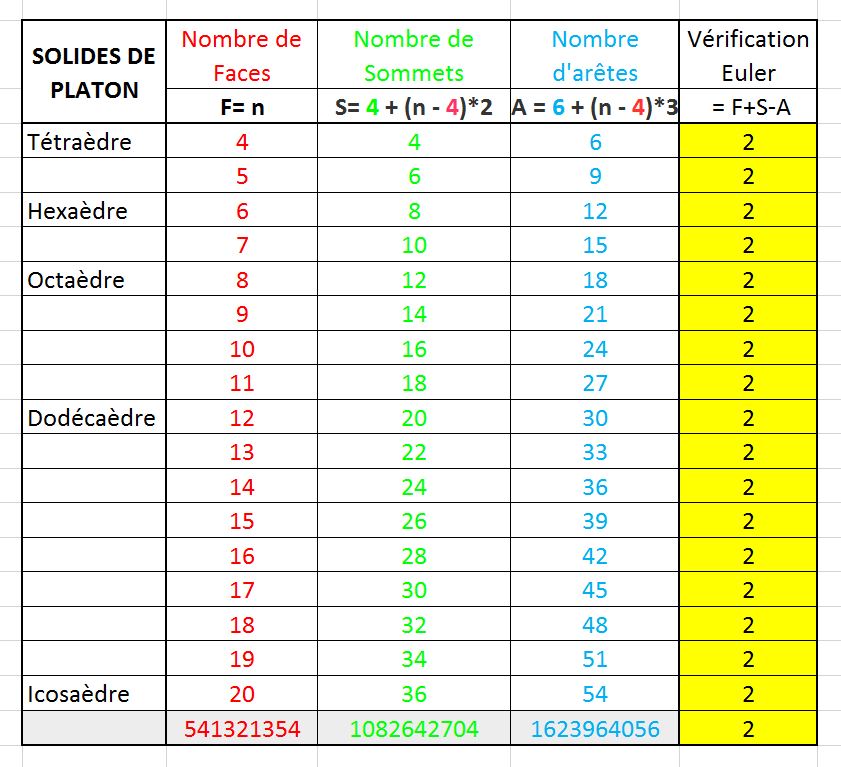 Bluffante la dernière ligne non? Ce message a été modifié par jumab le Jeudi 27 Août 2015 à 18h38 -------------------- Le signe de ton ignorance, c’est la profondeur de ta croyance en l’injustice et en la tragédie. Porté à mon attention par zone-7.net, auteur original Richard Bach dans le livre "Illusions-Récit d'un messie récalcitrant" |
|
Ecrit le: Jeudi 27 Août 2015 à 18h44

|
|
 Expert(e)       Groupe: Membres Messages: 2108 Membre n°: 10443 Inscrit le: 08/11/2013 |
Petites erreures dans ton tableau:
l'octaèdre n'a que 6 sommets, et 12 arêtes et l'icosaèdre, 12 sommets et 30 arêtes |
|
Ecrit le: Jeudi 27 Août 2015 à 18h49

|
|
|
Expert(e)       Groupe: Membres Messages: 519 Membre n°: 10713 Inscrit le: 06/02/2015 |
Arg tu as raison p'titjoule, mais il y a un lien logique qui traîne par là, je cherches...
-------------------- Le signe de ton ignorance, c’est la profondeur de ta croyance en l’injustice et en la tragédie. Porté à mon attention par zone-7.net, auteur original Richard Bach dans le livre "Illusions-Récit d'un messie récalcitrant" |
|
Ecrit le: Jeudi 27 Août 2015 à 19h13

|
|
 Expert(e)       Groupe: Membres Messages: 2108 Membre n°: 10443 Inscrit le: 08/11/2013 |
Oui, pourtant, c'est bien vu,
ça définit très bien trois des cinq solides... il y a peut être un truc a ajouter dans l'équation, une sorte de condition? |
|
Ecrit le: Jeudi 27 Août 2015 à 19h27

|
|
 Expert(e)       Groupe: Membres Messages: 310 Membre n°: 10787 Inscrit le: 15/08/2015 |
jumabonne aussi à cette recherche de la Fée du logique
Cette formule servirait-elle aussi pour les structures atomique de la matière ? Plongé dans la Chimie théorique et les minéraux, certaines infos me sautent aux yeux mais je ne comprends pas encore les liens. L'Allotropie me fait sourire et ça n'a rien à voir avec la Noobila nationale Le Diamant et Graphite sont composés tous les deux de Carbone mais structurés différemment au niveau atomique. Le Graphene est assez facilement réalisable à partir de graphite aussi et est très très rapide niveau conductivité électrique. Les formes géométriques de Platon me font penser aux structures atomiques. De la à imaginer produire du diamant pur fait maison, il n'y a qu'un pas Je mélange peut-être trop de choses, je partage quand même, montrez-moi mes erreurs siouplait ^^ Coté formules mathématiques, les Diagrammes de Phases présentent des choses intéressantes que j'espère utiles ici. Bon triturage de neurones -------------------- « Rien ne change tant qu'on n'y change rien »
|
|
Ecrit le: Jeudi 27 Août 2015 à 20h21

|
|
|
Expert(e)       Groupe: Membres Messages: 519 Membre n°: 10713 Inscrit le: 06/02/2015 |
Les solides de Platon vont tous par paires!
Tout est une question de Point de vue Dans mon tableau, prends les solides qui sont justes, inverses Face et Sommet, tadaaa!!! Tu trouves les solides qui manquent, l'Hexaèdre est l'inverse de l'Octaèdre, le Dodécaèdre de l'Isocaèdre, quand au Tétraèdre il n'a pas de parèdre, inverser 4 et 4 ne change rien! Mais c'est encore mieux que ça, j'ai compris que ma formule est super-puissante, elle ne s'occupe pas que des solides réguliers, convexes, etc, on peut vraiment qualifier tous les types de solides, quelle que soit leur géométrie, même les plus biscornus! En fait la seule erreur dans mon tableau a été d'inscrire à la va-vite Octaèdre et Icosaèdre en regardant uniquement le nombre de faces, mais sinon le reste est très propre! Mais les formules en soit peuvent nous amener très loin! Une mise au propre à venir... -------------------- Le signe de ton ignorance, c’est la profondeur de ta croyance en l’injustice et en la tragédie. Porté à mon attention par zone-7.net, auteur original Richard Bach dans le livre "Illusions-Récit d'un messie récalcitrant" |
|
Ecrit le: Vendredi 28 Août 2015 à 01h42

|
|
|
Expert(e)       Groupe: Membres Messages: 519 Membre n°: 10713 Inscrit le: 06/02/2015 |
Soit un polyèdre prismatique à n faces, avec n ≥ 4 (sinon ce n'est pas un polyèdre!)
Alors, S = 4 + (n - 4)*2 Et A = 6 + (n - 4)*3 De plus, pour tout polyèdre x qui vérifie la relation Fx + Sx - Ax =2, il existe un polyèdre dual y dont les proportions sont les suivantes: Fy = Sx Sy = Fx Ay = Ax Le résultat en tableau: 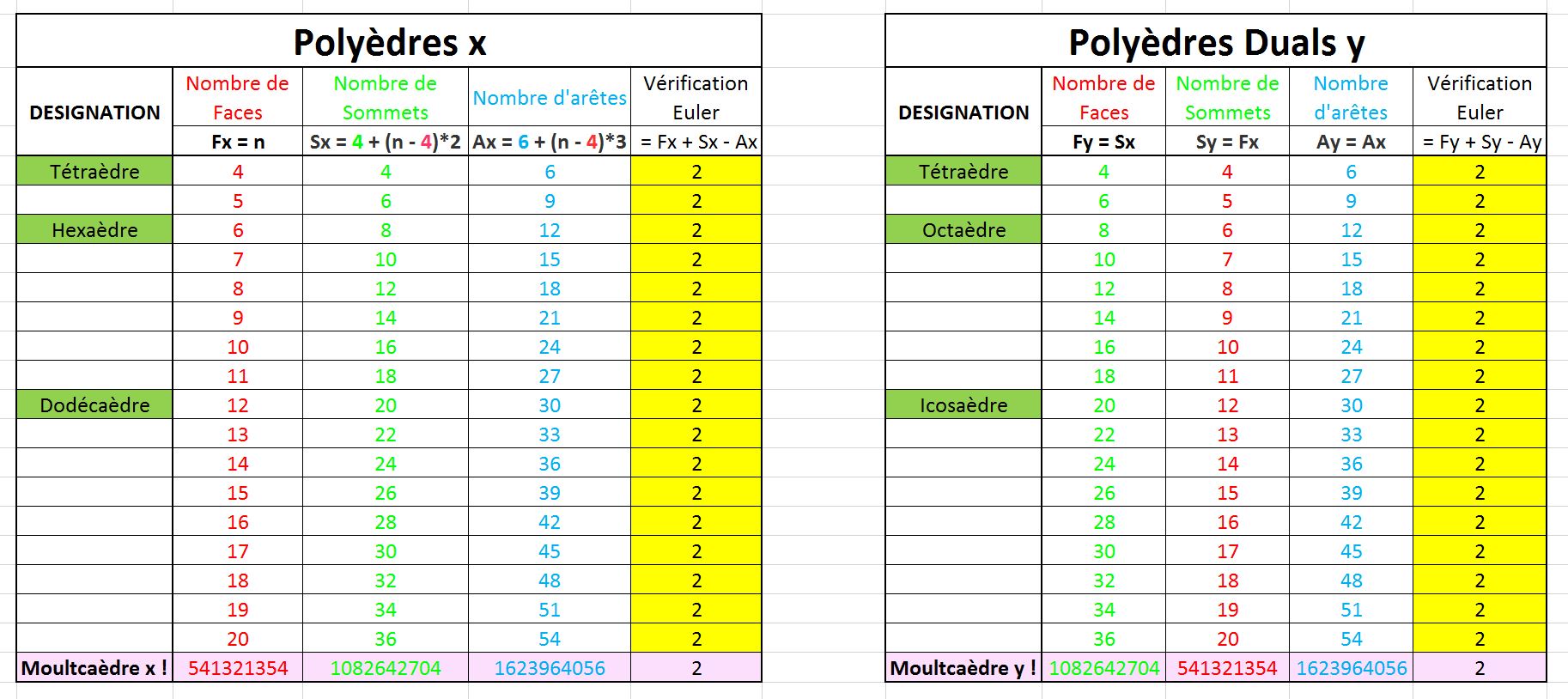 Bon ce n'est pas encore la panacée, il me manque les polyèdres anti-prismatiques, peut-être quelques autres bestioles bizarres, mais ces deux tableaux englobent une bonne partie du job! Je m'occuperais des anti-prismatiques un de ces 4, pour l'instant mon lit m'appelle! -------------------- Le signe de ton ignorance, c’est la profondeur de ta croyance en l’injustice et en la tragédie. Porté à mon attention par zone-7.net, auteur original Richard Bach dans le livre "Illusions-Récit d'un messie récalcitrant" |
|
Ecrit le: Vendredi 28 Août 2015 à 09h40

|
|
|
Expert(e)       Groupe: Membres Messages: 519 Membre n°: 10713 Inscrit le: 06/02/2015 |
Hello all !
Juste un petit message pour porter votre attention sur quelque chose que j'ai redécouvert, l'importance de la différence entre les polyèdres prismatiques et les polyèdres anti-prismatiques. Ces deux grandes familles ont chacune leurs polyèdres duaux respectifs: polyèdre prismatique simple: Prisme polyèdre prismatique dual: Diamant Polyèdre anti-prismatique simple: Antiprisme Polyèdre anti-prismatique dual: Trapézoèdre Intuitivement, il me semble que les antiprismes et trapézoèdres sont plus "stables", "beaux", "naturels", que les prismes et les diamants A l'instinct JamBonius, je dirais que c'est dans la famille des anti-prismes que nous devrions chercher les règles de construction de la nature! (chimie, organisation atomique, etc...) Edit: mmmh non encore mieux en fait, les polyèdres simples sont à chaque fois une méthode mathématique fictive de définitions de polyèdres bien réels, qui sont leurs duaux. Les diamants et les trapézoèdre semblent pouvoir être des éléments constitutifs, mais certainement pas les prismes ni les antiprismes! Ce message a été modifié par jumab le Vendredi 28 Août 2015 à 10h06 -------------------- Le signe de ton ignorance, c’est la profondeur de ta croyance en l’injustice et en la tragédie. Porté à mon attention par zone-7.net, auteur original Richard Bach dans le livre "Illusions-Récit d'un messie récalcitrant" |
|
Ecrit le: Vendredi 28 Août 2015 à 11h28

|
|
 Expert(e)       Groupe: Membres Messages: 2108 Membre n°: 10443 Inscrit le: 08/11/2013 |
et bien ça a l'air coule ta formule, c'est bien vu
Un peu d'historique sur les polyèdres http://culturemath.ens.fr/video/Dupas-poly...upas-chrono.htm https://fr.wikipedia.org/wiki/Hydrocarbure_de_Platon et un bon cite ici: http://www.spirit-science.fr/Matiere/cristal.html |
|
Ecrit le: Samedi 29 Août 2015 à 12h01

|
|
|
Expert(e)       Groupe: Membres Messages: 519 Membre n°: 10713 Inscrit le: 06/02/2015 |
Salut tout le monde!
Je vous invites à faire un tour sur ce site qui fourmille d'animation géométriques magnifiques! Ensuite je vous doit quelques explications sur la manière dont j'ai monté ma formule, cette dernière est imparable! La réflexion porte sur ce que j’appellerais les "pavages réguliers". Un pavage "régulier" est un pavage dans lequel chaque sommet est lié au même nombre d'arêtes (je me moque pas mal dans ma formule des aires respectives de chacune des faces, la réflexion porte uniquement sur la cohérence Arêtes/Sommets) Si nous y prêtons attention quelques secondes, nous allons rapidement trouver 2 types de pavages régulier, le premier est de degré 3 (3 arêtes joignent chaque sommet), le deuxième est de degré 4 (4 arêtes joignent chacun des sommets). Voici quelques exemples de pavages réguliers de degré 3:  Notez bien que ce que j'appelle "pavage régulier" ne concerne absolument pas les formes ou dimensions des faces, comme en témoigne le 3eme dessin! D'ailleurs, je vous prie de noter au passage que la 3eme figure ne peut fabriquer que 3 types de polygones, triangles, quadrilatères et pentagones... Maintenant quelques exemples de pavages réguliers de degré 4:  Notez au passage que cette méthode (degré 4) peut créer sur la figure 3 une infinité de polygones, je vous laisse imaginer la difficulté inhérente au travail dans pavage de degré 4 par rapport à celui de degré 3! Bien, maintenant que nous sommes à peu près d'accord sur ces 2 grands types de pavages, nous pouvons faire le lien avec la science des polyèdres! En effet, nos polyèdres aussi sont classés en deux grandes familles, les prismes et les antiprismes:  Vous l'aurez peut-être remarqué maintenant, les prismes correspondent à pavage de degré 3, tandis que les antiprismes correspondent à un pavage de degré 4! Donc si je suis capable de trouver une formule qui exprime le nombre d'Arêtes et de Sommets en fonction du nombre de Faces dans un pavage de degré 3, cette formule peut décrire 1 à 1 tous les prismes possibles, en fonction de leur nombre de face! En gros, comment ajouter une Face à un maillage de degré 3 sans en modifier la nature (degré 3)? Pour ce faire, je prends un extrait d'un maillage de degré 3 sous les yeux:  La face coloriée en bleu est celle sur laquelle je vais travailler, nous pouvons considérer qu'elle est unique, à condition cependant de ne pas omettre qu'elle est inséré dans un maillage de degré 3. Tout l'exercice consiste donc à scinder cette face unique en deux faces, le tout sans modifier la nature du maillage. Nous n'avons pas 36 solutions, tous les Sommets du maillage sont déjà "full", ils joignent tous 3 Arêtes, nous sommes obligé de créer deux nouveaux Sommets! Voici notre nouvelle face, qui n'a pas modifié la nature du réseau:  Remarque: j'ai scindé la face en deux parties égales, mais ces deux parties auraient pu être inégales! Maintenant, nous pouvons établir la suite qui se met en place à chaque fois que je rajoutes 1 Face à un réseau/maillage/pavage de degré 3:  Conclusion: +1F se traduit par +2S (en vert) et +3A (en rouge) C'est de là que vient ma formule, et si le nombre de face est supérieur à 4 le réseau peut être vu comme le plus simple des prisme, 5 le deuxième plus simple, etc... Du coup, on caractérise tous les prismes jusqu'à l'infini, et par extension leur duaux. Ce même travail très simple peut être fait sur les réseau de degré 4, et il caractérisera tous les antiprismes et leurs duaux. Mais ensuite, la plus belle partie du travail nous attend sur les pavages "semi-réguliers". Allez observer un pavage à base de pentagone, vous remarquerez que ce dernier possède à la fois des Sommets de degré 3 et des Sommets de degré 4, trouver le lien qui unit le nombre de chacun de ces Sommets me semble promettre de grandes choses... -------------------- Le signe de ton ignorance, c’est la profondeur de ta croyance en l’injustice et en la tragédie. Porté à mon attention par zone-7.net, auteur original Richard Bach dans le livre "Illusions-Récit d'un messie récalcitrant" |
|
Ecrit le: Samedi 29 Août 2015 à 12h40

|
|
|
Expert(e)       Groupe: Membres Messages: 519 Membre n°: 10713 Inscrit le: 06/02/2015 |
Edit: voir le post qui suit, sur la page 2, celui-ci n'est pas parfait.
Mmmh dans mon dernier post j'ai allègrement mélangé les termes "maillage", "pavage" et "réseau", car ils correspondent tous trois à une même opération, qui consiste à tirer des lignes sur une surface, afin de la diviser et d'en faciliter l'étude. Nous pourrions préciser ces trois termes de la manière suivante: Pavage régulier: toutes les Faces sont d'aire égales Réseau régulier: toutes les Arêtes sont de longueurs égales Maillage régulier: tous les Sommets respectent la même règle de construction (cf mon article précédent!) Ce message a été modifié par jumab le Samedi 29 Août 2015 à 17h22 -------------------- Le signe de ton ignorance, c’est la profondeur de ta croyance en l’injustice et en la tragédie. Porté à mon attention par zone-7.net, auteur original Richard Bach dans le livre "Illusions-Récit d'un messie récalcitrant" |
1 utilisateur(s) sur ce sujet (1 invités et 0 utilisateurs anonymes)
0 membres:
 Pages: (3) [1] 2 3 Pages: (3) [1] 2 3 |
   |
[ Script Execution time: 0.1100 ] [ 12 queries used ] [ GZIP activé ]









